아직 회원이 아니신가요?
회원가입 하기
- CBT 필기
- CBT 실기
-
자격증 필기 기출문제
- 네트워크관리사 1급
- 네트워크관리사 2급
- 디지털영상편집 1급
- 디지털영상편집 2급
- 리눅스마스터 1급
- 리눅스마스터 2급
- 물류관리사 1교시
- 물류관리사 2교시
- 유통관리사 1급
- 유통관리사 2급
- 유통관리사 3급
- 인터넷보안전문가 2급
- 전산회계운용사 1급
- 전산회계운용사 2급
- 전산회계운용사 3급
- 전자상거래운용사
- 컴퓨터활용능력 1급
- 컴퓨터활용능력 2급
- PC정비사 1급
- PC정비사 2급
- 가스기능장
- 가스산업기사
- 건설안전기사
- 건설안전산업기사
- 건축기사
- 건축산업기사
- 공조냉동기계기사
- 공조냉동기계산업기사
- 광학기사
- 교통기사
- 기계설계산업기사
- 기계정비산업기사
- 기상기사
- 대기환경기사
- 대기환경산업기사
- 배관기능장
- 사무자동화산업기사
- 산림기사
- 산림산업기사
- 산업안전기사
- 산업안전산업기사
- 설비보전기사
- 소방설비기사(기계)
- 소방설비산업기사(기계)
- 소방설비기사(전기)
- 소방설비산업기사(전기)
- 수질환경산업기사
- 신재생에너지발전설비기사
- 신재생에너지발전설비산업기사
- 에너지관리기능장
- 용접산업기사
- 위험물기능장
- 위험물산업기사
- 자동차정비기사
- 자동차정비산업기사
- 전기공사기사
- 전기공사산업기사
- 전기기능장
- 전기기사
- 전기산업기사
- 전자계산기조직응용기사
- 전자기사
- 전자산업기사
- 정보처리기사
- 정보처리산업기사
- 정보통신기사
- 정보통신산업기사
- 조경산업기사
- 컬러리스트기사
- 컬러리스트산업기사
- 화공기사
- 자격증 실기 기출문제
- 문의













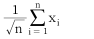
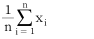
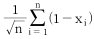
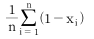
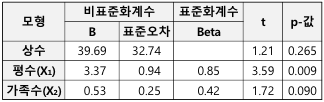
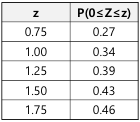
 )
)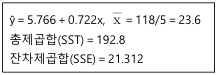

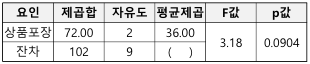
 )의 분포에 관한 설명으로 틀린 것은?
)의 분포에 관한 설명으로 틀린 것은?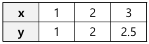
 은 n개 중에서 r개를 선택하는 조합의 수이다.)
은 n개 중에서 r개를 선택하는 조합의 수이다.)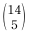
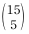
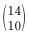
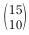
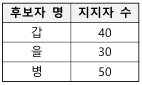
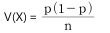
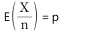
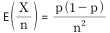
 를 추정하였다. 모비율에 대한 가설 H0:p=0.4 vs H1:p>0.4를 검정하기 위한 검정통계량은?
를 추정하였다. 모비율에 대한 가설 H0:p=0.4 vs H1:p>0.4를 검정하기 위한 검정통계량은?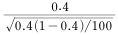
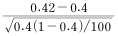
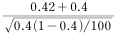
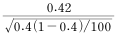
 에 대한 성질이 아닌 것은?
에 대한 성질이 아닌 것은?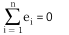
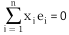
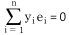
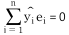

 라 하자. H0:μ=8 vs H1:μ=6.416의 검정을 위해 기각역을
라 하자. H0:μ=8 vs H1:μ=6.416의 검정을 위해 기각역을