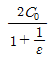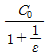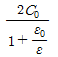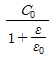15. 정전용량이 C0[F]인 평행판 공기 콘덴서가 있다. 이것의 극판에 평행으로 판간격 d[m]의 1/2 두께인 유리판을 삽입하였을때의 정전용량[F]은? (단, 유리판의 유전율은 ℇ[F/m]이라 한다.)
3
* 해설